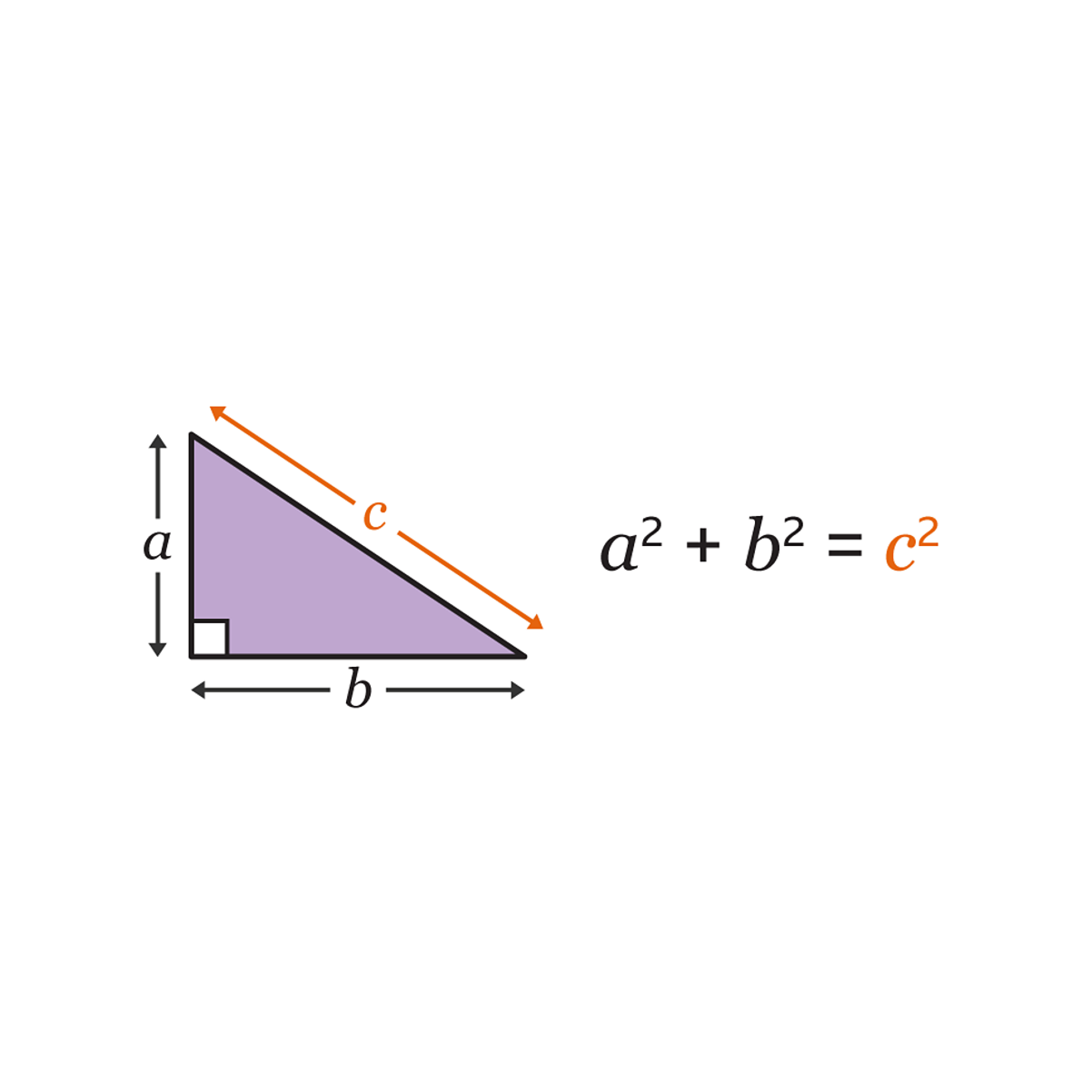GeometriaBásico

Entendendo (finalmente) o teorema de Pitágoras

25/05/2025

Provando o Teorema de Pitágoras através de Áreas: Uma Abordagem Visual e Intuitiva

Introdução

O Teorema de Pitágoras é um dos resultados mais famosos e importantes da matemática. Atribuído ao matemático grego Pitágoras (570-495 a.C.), este teorema estabelece uma relação fundamental entre os lados de um triângulo retângulo. Embora existam mais de 350 demonstrações diferentes deste teorema ao longo da história, neste artigo vamos focar em uma das mais elegantes e intuitivas: a prova geométrica usando áreas.

Requisitos

Esta demonstração tem a vantagem de ser visualmente clara e não depender de manipulações algébricas complexas, tornando o teorema acessível mesmo para quem está começando seus estudos em geometria.

Se você não entender tudo, não se preocupe. Tente compreender os princípios gerais. Isso fará com que você memorize mais facilmente o resultado e também poderá usar os princípios utilizados, como a decomposição de áreas, para resolver outros problemas.

Além disso, toda a base para o entendimento deste assunto e temas mais corriqueiros de vestibular está em nosso curso Matemática Fuvest e ENEM.

Enunciado do Teorema

O Teorema de Pitágoras relaciona o tamanho do maior lado de um triângulo retângulo (hipotenusa) com os demais lados (catetos). Ele pode ser enunciado formalmente da seguinte maneira:

Em qualquer triângulo retângulo, o quadrado da medida da hipotenusa é igual à soma dos quadrados das medidas dos catetos.

Em termos algébricos, se temos um triângulo retângulo com catetos de medidas a e b, e hipotenusa de medida c, então:

a² + b² = c²

Abaixo segue um triângulo retângulo:

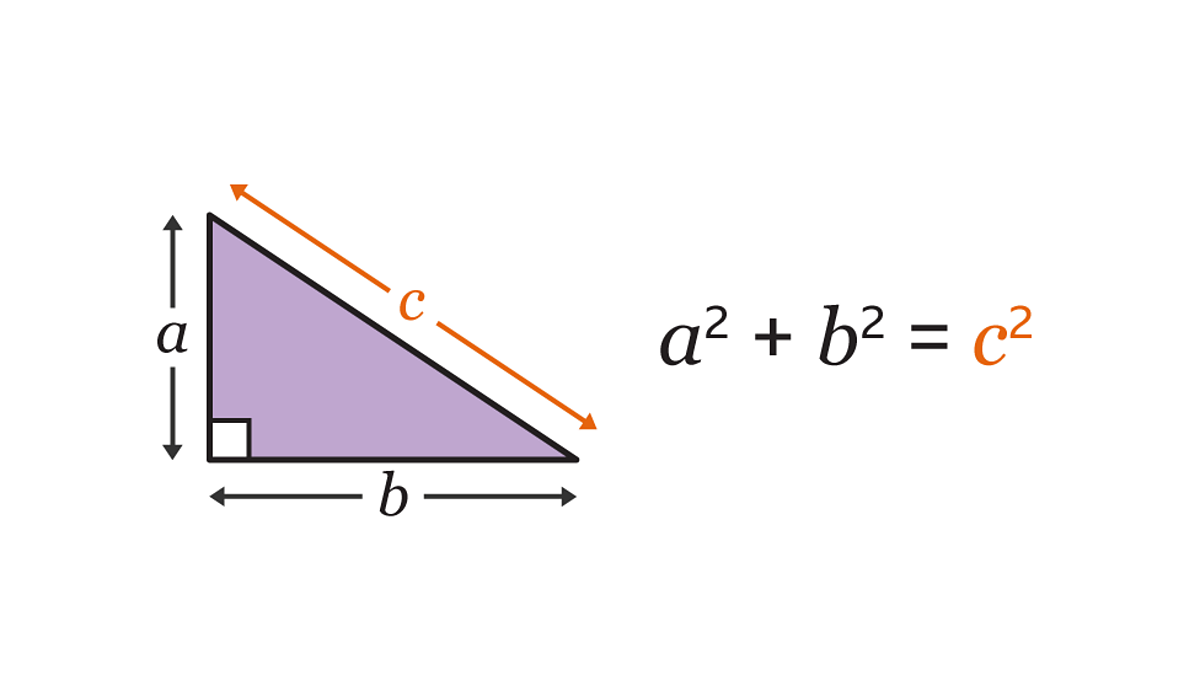
Observe que neste triângulo:

• O cateto a é o lado vertical.
• O cateto b é a base horizontal.
• A hipotenusa c conecta os extremos dos catetos.

Este teorema é fundamental em diversos campos da matemática e suas aplicações, desde a geometria euclidiana até a física, engenharia, arquitetura e navegação. Ele permite calcular distâncias, verificar perpendicularidade e resolver problemas geométricos complexos.

Demonstração Geométrica

Por hipótese, assumimos que temos um triângulo retângulo de vértices , e , sendo o ângulo reto (90 graus). O lado tem tamanho e o lado tem tamanho , conforme a figura abaixo.

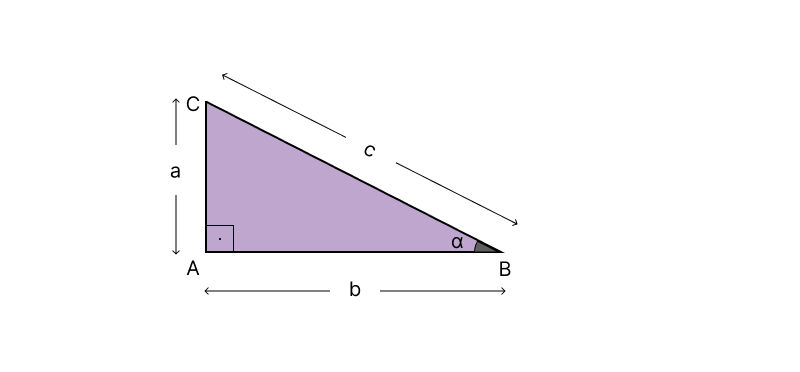
Agora o que vamos fazer é estender até de forma que tenha tamanho , conforme figura abaixo.

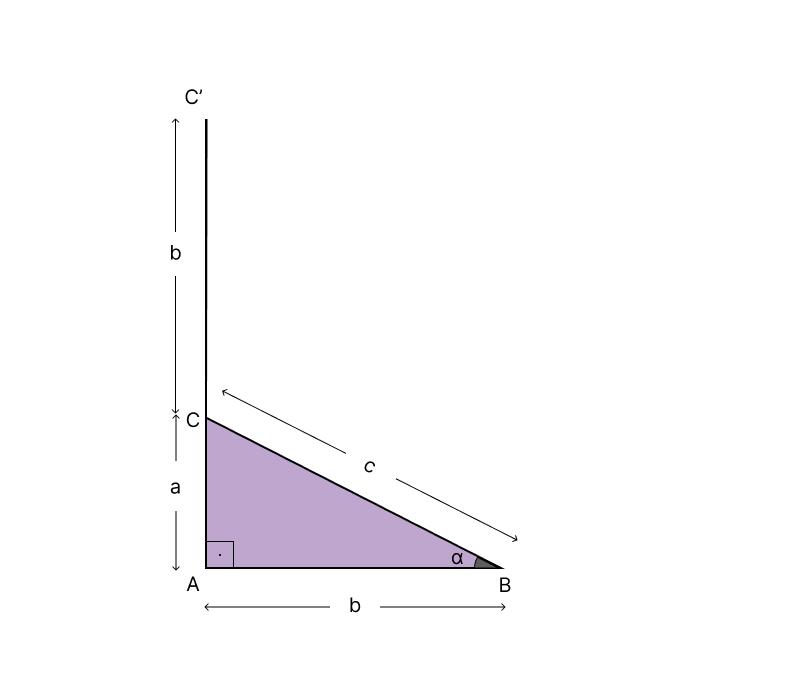
Além disso, desenhamos um quadrado de lado sobre a hipotenusa e obtemos os pontos e como vértices do quadrado . Por fim, conectamos e para obter um novo triângulo , conforme figura abaixo

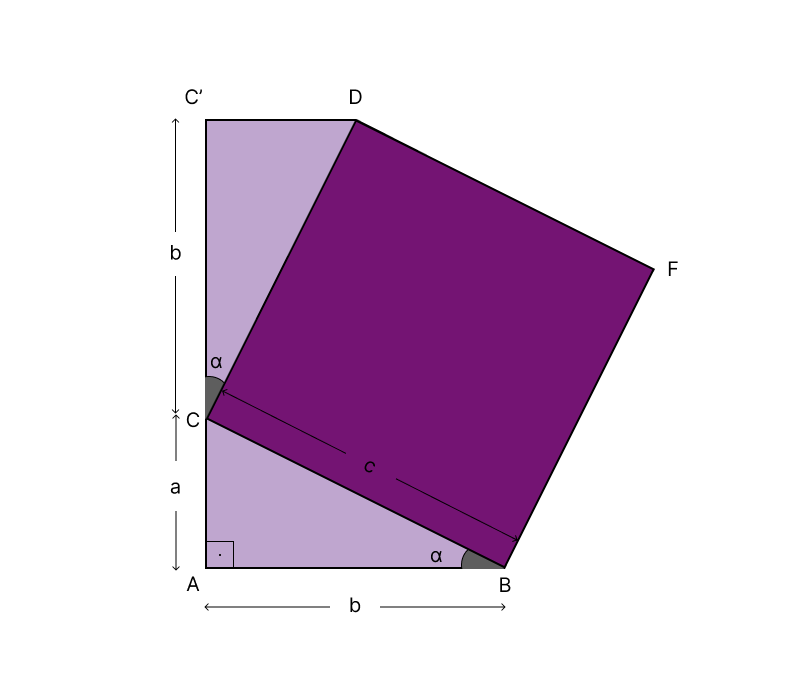
Depois estendemos o lado até de forma que tenha medida . Daí, obtemos um novo triângulo .

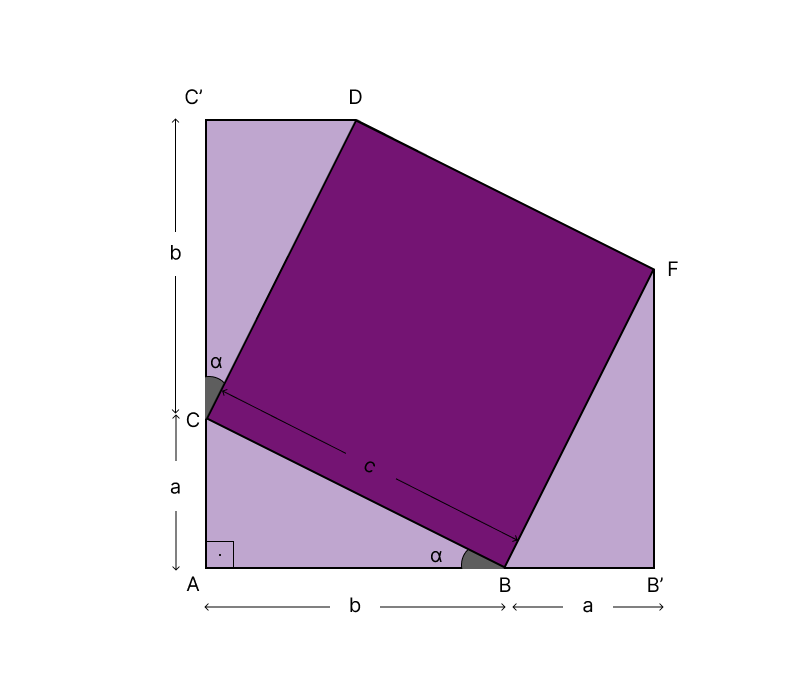
A equivalência dos triângulos

Esses três triângulos são equivalentes. Vejamos a razão disso ser verdade. Primeiro, note que os ângulos que estão na reta devem somar , logo:

Porém, o é , pois é o ângulo de um quadrado.

Além disso, como a soma dos ângulos de um triângulo é , a soma dos ângulos do triângulo deve ser:

Portanto, aplicando na equação anterior para encontrar , temos:

Daí:

Note, portanto, que os triângulos e são equivalentes por lado, ângulo, lado, uma vez que ambos possuem um ângulo de entre lados que medem e .

Existem algumas cláusulas diferentes de equivalência de triângulos, mas não é necessário decorar nenhuma delas. Não vamos explicar isto aqui para não deixar o artigo longo, mas se você fizer um bom curso ou ler um bom livro didático, ele provavelmente buscará fazer com que você entenda os casos de equivalência em vez de apenas decorá-los.

De forma análoga o triângulo é equivalente ao . Desta forma obtemos que

e que

Assim, estentendo agora as retas e obtemos o ponto como interseção, conforme figura abaixo.

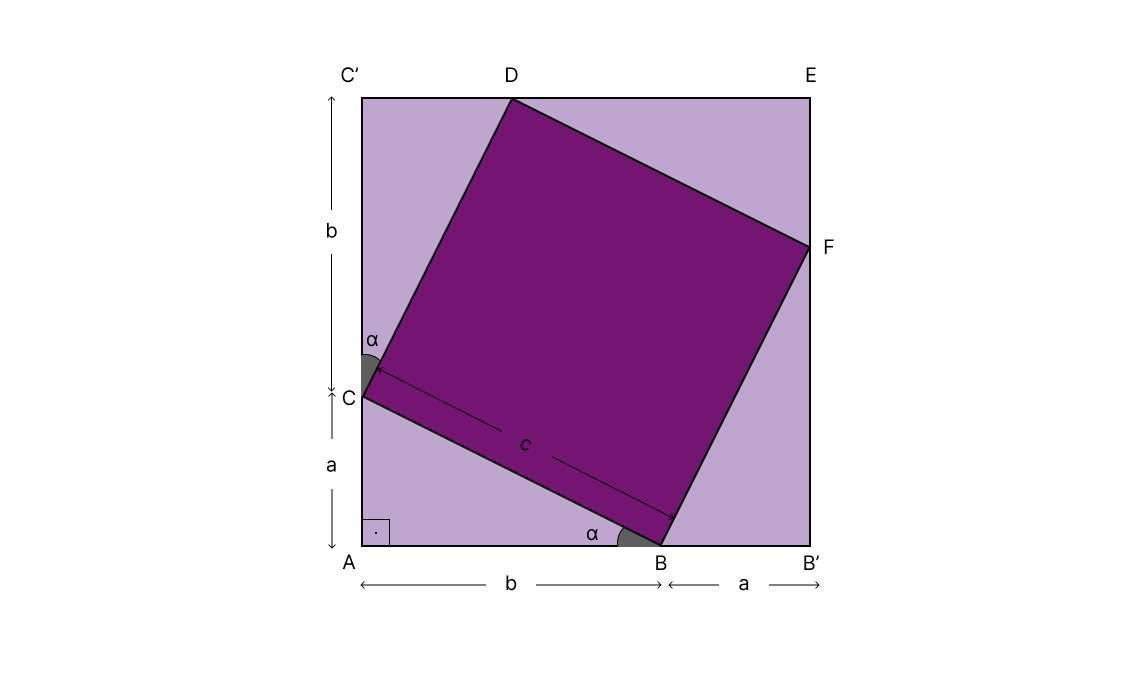
Por paralelismo obtemos que

e que o triângulo possui ângulos , e . Logo é retângulo de hipotenusa de tamanho e por ângulo, lado, ângulo é equivalente ao triângulo .

Dessas equivalencias temos que também é um quadrado pois todos os ângulos são retos e todos seus lados são iguais

Sobreposição de áreas

Note que a área do quadrado maior é a soma da área do quadrado menor e dos quatro triângulos retângulos equivalentes, onde cada um possui área .

Logo,

Além disso,

• A área do quadrado menor de lado é .
• A área de cada um dos triângulos cinza é metade do produto entre base e altura, isto é, .
• A área do quadrado maior de lado é .

Daí temos que

Conclusão

Esta demonstração geométrica do Teorema de Pitágoras, baseada em áreas, oferece uma compreensão visual e intuitiva deste importante resultado matemático. Em vez de apenas memorizar a fórmula a² + b² = c², podemos entender sua veracidade e aplicar as técnicas utilizadas para resolver outras questões.

Gostou do conteúdo? Temos outros conteúdos básicos e avançados focados nos vestibulares em nosso curso Matemática Fuvest e ENEM.