Aproximando raízes quadradas
Introdução
Em algumas situações, como em provas de vestibulares, pode ser necessário calcular manualmente o valor de raízes quadradas. Um exemplo disso foi uma questão da FUVEST onde o candidato precisava calcular
A seguir vamos mostrar como calcular raizes quadradas com uma boa aproximação de forma rápida. Toda a base para o entendimento deste assunto e temas mais corriqueiros de vestibular estão em nosso curso Matemática Fuvest e ENEM.
A aproximação
Uma aproximação que não é tão conhecida é a seguinte:
Mas antes de decorar, vamos entender por que essa aproximação faz sentido. O entendimento vai facilitar a memorização e, em caso de esquecimento, vai possibilitar que você chegue sozinho ao resultado caso haja necessidade.
Racional
Podemos reescrever
Mas se tomarmos
Logo, se
Exemplo 1
Calcule o valor aproximado de
Solução: Pela aproximação temos que
Note que o resultado obtido com uma calculadora foi muito próximo ao da nossa aproximação. De fato, o erro percentual
da aproximação foi de
Exemplo 2
Calcule rapidamente o valor aproximado de
Solução: Para achar a raiz, precisamos achar primeiro o número inteiro que elevado ao quadrado é mais próximo de
mas como 529 é o quadrado perfeito mais próximo de 520, devemos fazer o seguinte
Tomando
Encontramos, portanto, que
porém o valor real é
Quando é possível usar a fórmula de aproximação
Nem sempre será possível aplicar a fórmula, pois os erros começam a ficar inaceitáveis dependendo da magnitude de
| -0.5 | 0.70711 | 0.75 |
| -0.4 | 0.77460 | 0.80 |
| -0.3 | 0.83666 | 0.85 |
| -0.2 | 0.89443 | 0.90 |
| -0.1 | 0.94868 | 0.95 |
| 0.0 | 1.00000 | 1.00 |
| 0.1 | 1.04881 | 1.05 |
| 0.2 | 1.09545 | 1.10 |
| 0.3 | 1.14018 | 1.15 |
| 0.4 | 1.18322 | 1.20 |
| 0.5 | 1.22474 | 1.25 |
Tais desvios também podem ser vistos no gráfico abaixo:
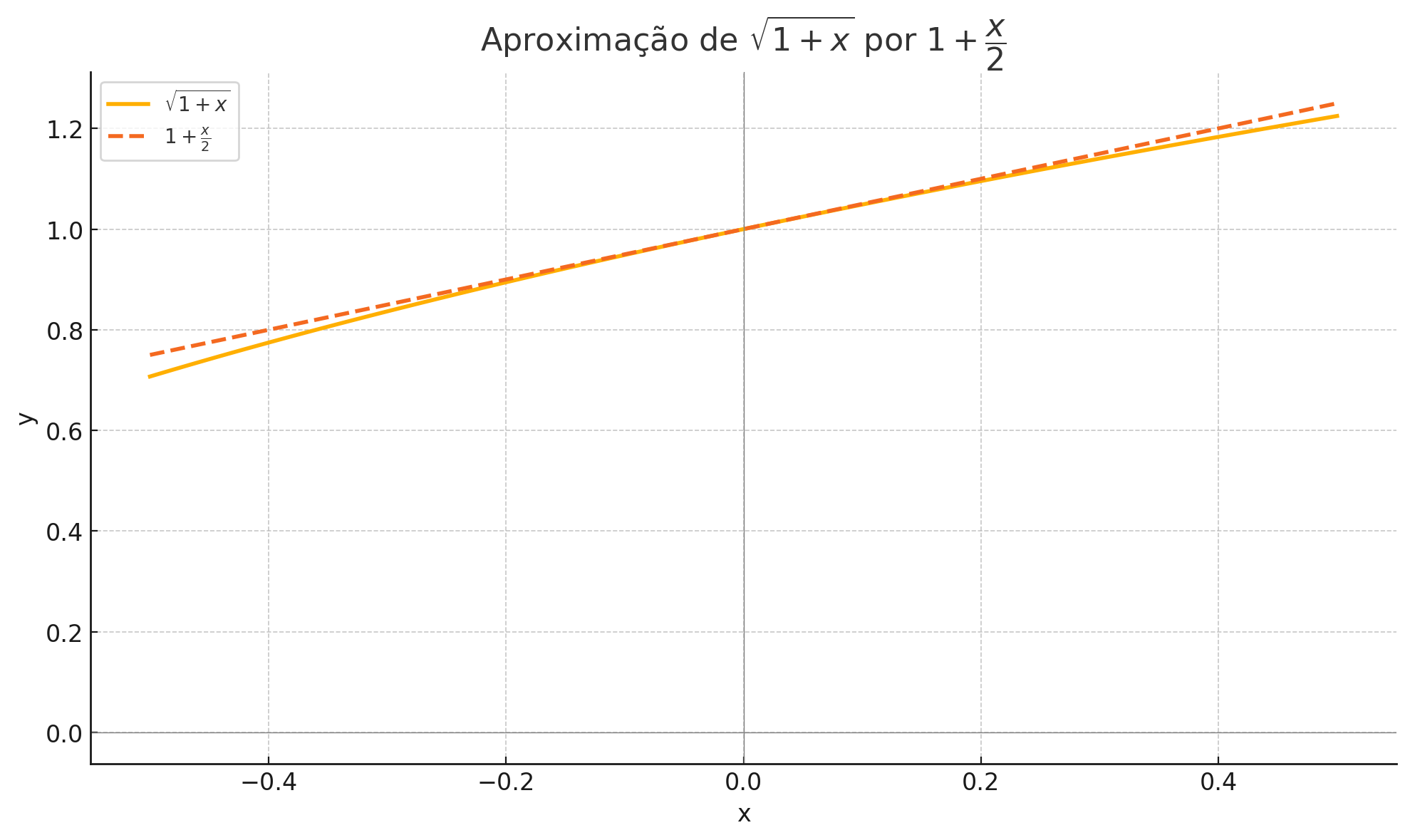
Conclusão
A aproximação