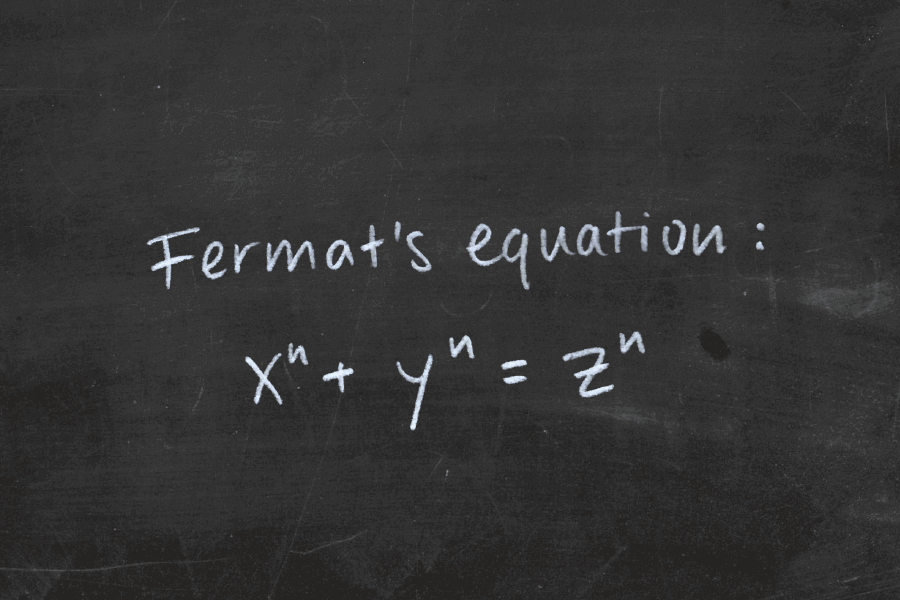ÁlgebraTeoria dos NúmerosIntermediário

Introdução à Teoria dos Números

14/04/2025

Teoria dos Números

1. Introdução

Contexto

A Teoria dos Números é um ramo da matemática que pode ser considerada de nível avançado pois muitas vezes só é ensinado em cursos de nível superior nos cursos onde há maior necessidade do estudo de Matemática Teórica.

Este artigo, porém, se limita ao básico do assunto. Para um conteúdo mais avançado sobre o assunto favor ler o artigo avançado sobre Teoria dos Números.

Aplicações práticas do assunto

As aplicações mais comuns da teoria dos números são encontradas em áreas como criptografia, teoria da computação, algoritmos e segurança da informação. Por exemplo, a criptografia RSA, amplamente utilizada para proteger dados na internet, baseia-se em propriedades de números primos e fatoração. Além disso, a teoria dos números é usada em sistemas de codificação, compressão de dados e geração de números pseudoaleatórios, sendo essencial para o desenvolvimento de tecnologias modernas.

O Último Teorema de Fermat é um dos problemas mais famosos da Teoria dos Números. Ele afirma que não existem números inteiros positivos , e que satisfaçam a equação para qualquer inteiro . Este teorema foi conjecturado por Pierre de Fermat em 1637, mas permaneceu sem demonstração por mais de 350 anos. Somente em 1994, o matemático Andrew Wiles, com a ajuda de Richard Taylor, conseguiu provar o teorema utilizando ferramentas avançadas da Teoria dos Números e da Geometria Algébrica. A demonstração é considerada um marco na história da matemática.

No vestibular

Os conteúdos deste artigo podem ser cobrados no vestibular, mas normalmente são usados de forma indireta como no cálculo de um MDC ou para decompor um número em seus fatores primos

2. Conteúdo

Divisibilidade

Um número inteiro é divisível por outro número inteiro (com ) se existe um número inteiro tal que . Nesse caso, dizemos que é um divisor de .

Exemplo:

• é divisível por , pois .
• não é divisível por , pois não existe um inteiro tal que .

Algoritmo da Divisão

Dado dois números inteiros onde , existem inteiros (quociente) e (resto) únicos tais que:

Exemplo:
Dividindo por :

• (quociente) e (resto), pois .

Máximo Divisor Comum (MDC)

O máximo divisor comum (MDC) de dois números inteiros e é o maior número inteiro que divide ambos e sem deixar resto.

Exemplo:

• O MDC de e é , pois é o maior número que divide e .

Algoritmo de Euclides

O Algoritmo de Euclides é um método eficiente para calcular o MDC de dois números inteiros e . Ele se baseia na seguinte propriedade:

onde é o resto da divisão de por .

Exemplo:
Calcular o MDC de e :

1. (quociente) e (resto).
2. (quociente) e (resto).
3. (quociente) e (resto).
   O MDC é .

Números Primos

Um número primo é um número inteiro maior que que possui exatamente dois divisores: e ele mesmo.

Exemplo:

• são números primos.
• não é primo, pois é divisível por e .

Critérios de Divisibilidade

Os critérios de divisibilidade são regras que permitem verificar rapidamente se um número é divisível por outro.

Divisibilidade por 2

Um número é divisível por se seu último dígito for par (0, 2, 4, 6, 8).

Exemplo:

• é divisível por , pois termina em .
• não é divisível por , pois termina em .

Divisibilidade por 3

Um número é divisível por se a soma de seus dígitos for divisível por .

Exemplo:

• : , que é divisível por .
• : , que não é divisível por .

Divisibilidade por 5

Um número é divisível por se terminar em ou .

Exemplo:

• é divisível por , pois termina em .
• não é divisível por , pois termina em .

Divisibilidade por 7

Para verificar a divisibilidade por , dobre o último dígito, subtraia-o do número formado pelos demais dígitos e veja se o resultado é divisível por .

Exemplo:

• : , que é divisível por .
• : , que não é divisível por .

Divisibilidade por 9

Um número é divisível por se a soma de seus dígitos for divisível por .

Exemplo:

• : , que é divisível por .
• : , que não é divisível por .

Divisibilidade por 11

Um número é divisível por se a diferença entre a soma dos dígitos de posição ímpar e a soma dos dígitos de posição par for divisível por .

Exemplo:

• : , que é divisível por .
• : , que não é divisível por .

3. Conclusão

A Teoria dos Números é um campo fascinante que fornece ferramentas essenciais para entender as propriedades dos números inteiros. Conceitos como divisibilidade, números primos e o algoritmo de Euclides têm aplicações práticas em diversas áreas, incluindo criptografia e ciência da computação.