Como se vestir bem, economizar e acertar questões no vestibular
1. Introdução
Cada pessoa tem seu próprio estilo: o que é bonito para um pode não agradar tanto a outro. Mas, independentemente do seu gosto, é possível seguir princípios gerais para se vestir bem e economizar — e a matemática pode te ajudar nisso!
2. Princípio da contagem
O princípio da contagem, ou princípio multiplicativo, é fundamental na combinatória. Ele afirma: quando você tem várias etapas independentes e quer saber de quantas maneiras pode realizar todas elas, basta multiplicar o número de opções de cada etapa.
Por exemplo: se você tem 5 camisetas e 3 calças, para cada camiseta você pode escolher qualquer uma das 3 calças. Então, o total de combinações é 5 × 3 = 15.
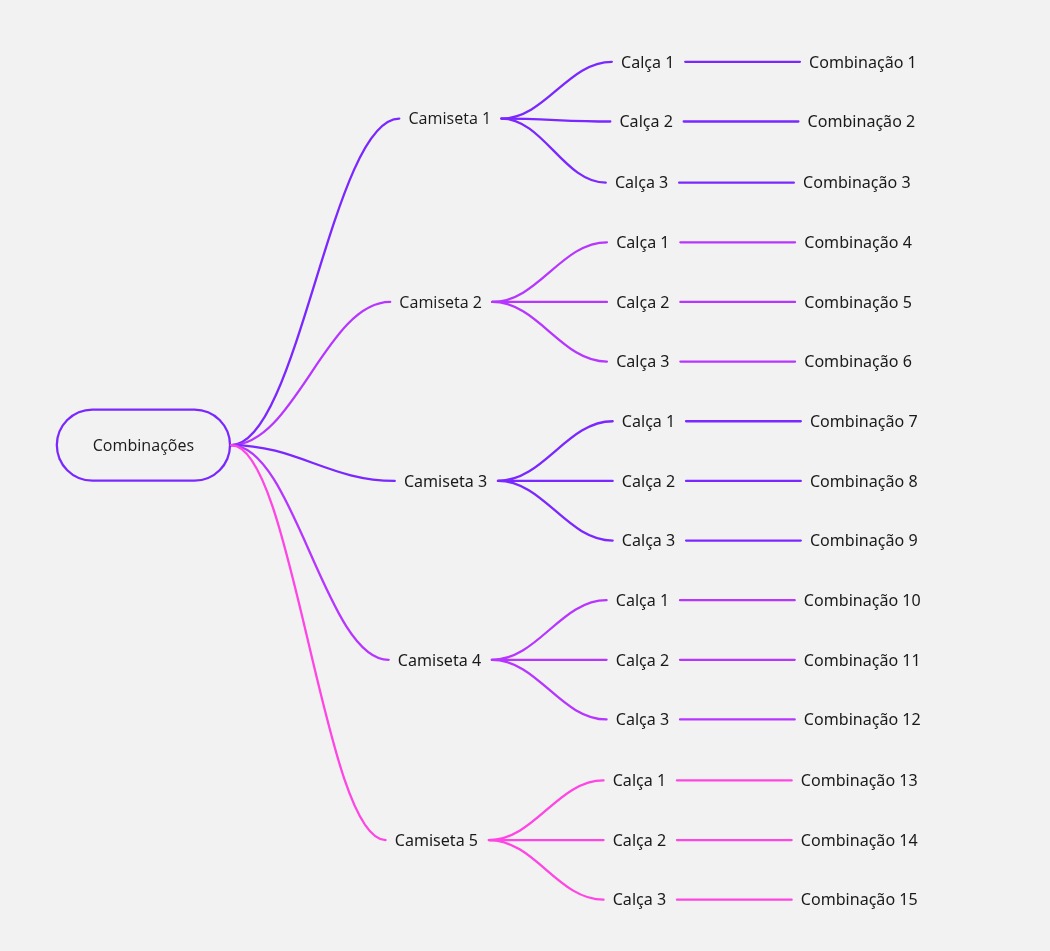
Esse princípio aparece em várias situações do dia a dia e é muito cobrado em provas de vestibular, especialmente em questões de arranjos, combinações e problemas de organização.
3. Ordenação
Às vezes, além de escolher as peças, a ordem em que você as usa importa. Por exemplo, se você quer saber de quantas maneiras pode organizar 4 camisetas diferentes em uma pilha no seu armário, está lidando com um problema de ordenação.
Exemplo: Se você tem 4 camisetas e quer saber de quantas formas pode organizá-las em uma pilha:
- A primeira posição pode ser ocupada por 4 camisetas (4 possibilidades)
- A segunda posição pode ser ocupada por 3 camisetas, já que uma não está mais disponível (3 possibilidades)
- A terceira posição pode ser ocupada por 2 camisetas, já que duas não estão mais disponíveis (2 possibilidades)
- A quarta posição pode ser ocupada por 1 camiseta, já que três não estão mais disponíveis (1 possibilidade)
Ou seja, existem 24 maneiras diferentes de ordenar as 4 camisetas.
De forma geral, o número de formas de ordenar
Chamamos esse produto de fatorial de n. O fatorial de um número
Use fatorial sempre que a ordem dos itens fizer diferença!
4. Combinação: escolhendo sem se importar com a ordem
Agora, imagine que você vai viajar e só quer levar 2 camisetas das 5 que tem. Aqui, a ordem em que você escolhe não importa — só importa o conjunto de camisetas escolhidas. Esse é um caso de combinação.
Exemplo: Se você tem 5 camisetas e quer escolher 2 para levar:
- Tem 5 possibilidades para a primeira camiseta
- Tem 4 possibilidades para a segunda camiseta
- Pode ordenar as camisetas de
formas
Logo, tem
De forma geral, é possível usar a seguinte fórmula para escolher
Ao dividir pelo fatorial do número de itens escolhidos, você elimina as repetições causadas pela ordem.
Dica de prova: Sempre que o enunciado pedir o número de maneiras de combinar itens de grupos diferentes (camisetas, calças, sapatos...), pense no princípio multiplicativo: multiplique as opções de cada grupo. Se a ordem não importar, use a fórmula da combinação.
5. Como economizar nas roupas
Agora que você já entendeu como a matemática pode ajudar a multiplicar seus looks, veja como montar um armário cápsula pode ser vantajoso para o bolso e para o dia a dia.
O armário cápsula é uma seleção enxuta de roupas versáteis, que combinam entre si e atendem a todas as suas necessidades do dia a dia.
Ao comprar uma nova roupa, prefira:
- Peças atemporais ao invés de roupas da moda, que podem ser usadas poucas vezes
- Peças que possam durar mais. Escolher uma peça de R$ 100,00 que vai durar por 10 anos pode ser mais vantajoso que uma de R$ 30,00 que só vai durar um ano
- Peças que combinem entre si. Isso é possível escolhendo roupas com base em uma paleta de cores que faça sentido para você. Um exemplo é o da figura abaixo
- Peças que você realmente vai usar. Exemplo: roupas confortáveis para estudar e fazer a prova do vestibular

Lembrando que cada pessoa tem seu estilo, então escolha a paleta de cores de acordo com suas preferências.
6. Exemplo de questão
(FUVEST-2010) Seja
Solução: Considerando que é possível que sobrem bolas, temos os seguintes cenários:
- Se Luís ficar com
bolas, necessariamente Antônio vai ficar com 0 (1 possibilidade) - Se Luís ficar com
bolas, Antônio vai ficar com ou bola (2 possibilidades) - Se Luís ficar com
bolas, Antônio vai ficar com , ou bolas (3 possibilidades) - ...
- Se Luís ficar com
bolas, Antônio vai ficar com um número que varia entre e bolas ( possibilidades)
Logo, o resultado é:
que, pelo estudo de sequências, é:
7. Conclusão
Organização, economia e matemática podem andar juntas! Ao montar seu armário cápsula, você não só facilita sua rotina como também pratica um conceito fundamental para o vestibular. Agora, que tal olhar para o seu guarda-roupa e calcular quantos looks diferentes você pode criar? E lembre-se: praticar questões de combinatória é tão importante quanto escolher a roupa certa para o dia da prova!
Se você quer dominar combinatória, arranjos, permutações e muito mais para gabaritar matemática no vestibular, recomendo o nosso curso completo:
Bons estudos e boas combinações — de looks e de acertos na prova!
